그 유명한 지구라트들 중 하나가 현재 비르스-님루드(Birs-nimrud)라 불리고 있는 옛 성(城) 보르십파(Borsippa) 성 안에 위치했던 에지다(Ezida) 신전탑이다. (153.1)
이 성은 영국인 리취(Claudius James Rich, A.D. 1787-1821)에 이어, 설형 문자를 최초로 판독한 롤린슨(Henry Creswick Rawlinson, A.D. 1810-1895) 경이 과학적으로 탐사했다. 그 뒤 1850년에 레이어드(Austen Henry Layard, A.D. 1817-1894)가, 그리고 1854년에 그의 조수였던 터키인 고고학자 라삼(Hormuzd Rassam, A.D. 1826-1910)이 각각 영국박물관의 지원을 받아 발굴했었다. (153.2)
이들 중 리취를 제외한 그 외 고고학자들에 의해 이 폐구에서 상당량의 점토판들이 출토되었는데, 거의 다 롤린슨 경과 그의 제자들에 의해 판독되었다. 판독된 비명 중 하나는 다음과 같은 내용의 비문으로 구약 성경에도 언급된 느부갓네살(Nebuchadnezzar, 재위 605-562 B.C.) 왕의 원기둥 비명이었다: (153.3)
“선왕이 세운 보르십파 탑은 꼭대기가 미완성인 채 42규빗(19m)의 높이로 세워져 오랫동안 폐허로 있었다. 배수 시설이 되어있지 않아 빗물이 벽돌을 쓸어내어 지붕이 파괴되었다. 마르둑 신이 나에게 재건하라고 명령했다. 나는 그 위치나 기초를 바꾸지 않았다. 적당한 시기에 나는 벽돌과 지붕을 보수하고 그 처마 밑에 내 이름을 쓰게 했다. 나는 이것을 그때의 모습대로 다시 세웠다.”47)
이 지구라트는 롤린슨 경이 발표한 보고서에 의해 그 전체적인 모형이 알려졌는데 오덤 교수가 간결하게 다음과 같이 요약했다: (153.5)
“이 거대한 탑은 천연 벽돌로 이루어진 대 위에 똑바로 세워졌는데, 몇 피트 위로 둘레가 평평히 수평지게 한 층계형으로 되어있다. 그 대 위에 똑바로 세워진 첫번째 층대는 정확히 각 변이 272피트 정방형이고, 높이는 26피트였다. 바로 이 첫 층대 위에 두번째 층대가 세워졌는데, 그것의 높이는 첫번째의 것과 같고, 각 변이 230피트의 정방형이었다. 이 둘째 층대는 첫 번째 층대의 중앙에 정확히 세워진 것이 아니라, 남서쪽 변의 모서리보다 북동쪽의 모서리에서부터 더 멀찍이 떨어져 세워졌다. 그렇기 때문에 그 위치는 한편은 12피트 안쪽으로, 다른 편은 30피트 안쪽으로 놓였다. 두번째 층대 위에 세워진 셋째 층대는 역시 높이가 26피트이고 각 변이 188피트의 정방형이었다. 건축물의 일률적인 모형이 설계도상 균형 지도록 네번째의 것부터는 높이가 26피트 대신에 약 15피트 높이의 층대로 달라졌다. 환언하면 네 번째의 것은 각 변이 146피트의 정방형으로서 아래의 층대들과 조화되도록 균형지게 감소되었다. 다섯째 층대는 각 변이 105피트의 정방형이고, 여섯째는 한 변이 62피트이고, 일곱째는 한 변이 20피트이며, 그 세 개 모두의 높이는 15피트씩이었다. 일곱째 층대 꼭대기 위에는 사당이 세워졌다. 이렇게 해서 그 전체적인 구조는 기초 위에서 3피트의 높이로 천연 벽돌 대를 포함해서 약 156피트의 높이가 되리라고 평가된다.”48)

바벨론 지구라트의 모형도
오덤 교수는 계속해서, 그의 논문에서, 이 거대한 신전 탑의 구조와 그 모형을 두고 직접적으로 “이 신전은 곧 우주에 배열된 태양계에 대한 이교도들의 관념에 따른 모형이었다”고 평하면서 옥스퍼드 대학교 고대사 교수 롤린슨(George Rawlinson, A.D. 1812-1902, H. C. Rawlinson 경의 동생)이 설명한 것을 아래와 같이 인용하였다: (155.1)
“이 멋진 건물의 장식들은 주로 그 의미 심장한 색채에 있었다. 일곱 층대들은 일곱 공간을 대표했는데, [고대 갈대아인의 점성술에 의하면] 그 공간에의 일곱 혹성들의 움직임이었다. 실지로 전해온 근거에 따르면, 오랜 옛적부터 이들 각 혹성들에게 그 성미에 따라 그들에게 그의 독특한 고유의 색깔이나 빛깔을 지정해 주었었다. 그래서 태양은 황금색, 달은 은색, 거의 빛의 영역에서 저 건너편에 멀리 떨어져 있는 토성은 흑색, 목성은 오렌지 색, 불꽃 빛나는 화성은 적색, 금성은 엷은 황색, 수성은 짙은 하늘색을 지정해 주었었다.”49)
이들 혹성신에게 주어졌던 그 고유의 색깔들이 각각 그 혹성신에게 지정된 7층 신전탑인 지구라트에 층대 별로 색칠해서 개개의 혹성신 제단들이 구별지어졌다. 롤린슨 교수는 이 지구라트의 각 층대와 개개의 혹성신과의 관련성에 대해서, 그리고 혹성신 별로 나타내는 층대의 색채에 대해서 다음과 같이 증언했다: (155.3)
“토성(Saturn-Nin-Girsou, Nin-ib 또는 Adar)에게 할당된 제일 밑 층대는 그 석조 표면에다 역청을 흠뻑 발랐기 때문에 새까맣게 되었다. 목성(Jupiter, Marduk)에게 지정된 둘째 층대는 구운 벽돌 그 자체 빛깔로 표면을 오렌지 빛 색깔을 내어 자기의 것으로 했다. 화성(Mars, Nergal)에게 지정된 셋째 층대는 반쯤 구운 벽돌을 사용해서 밝은 진흙의 적색을 내도록 해서 피의 붉은 색을 내게 했다. 태양(Sol, Shamash)에게 주어진 넷째 층대는 실제로 얇은 황금판을 입혀서, 그 자체의 빛깔을 내게 했다. 금성(Venus, Nebo)에게 할당된 여섯째 층대는 투화 시켜서 하늘이 보이도록 하여 하늘색을 내게 했다. 그리고 달(Luna, Sin)에게 지정된 일곱째 층대는 아마 넷째 층대처럼 실제로 금속판을 입혀서 은색을 내게 했던 것이다.”50) (156.1)
마치 일곱 무지개 색깔이 연상된다. 이 지구라트에 칠해진 색깔을 통해서 갈대아 사람들은 천공에 나타난 일곱 혹성들의 형상들을 한 눈으로 볼 수 있게 했다. (156.2)
4. 7층 신전탑에 나타난 천동설
죠지 롤린슨 교수의 설명에 따르면, 제일 아래 층, 그러니까 지구라트의 첫째 층대를 토성 닌-이브 신에게 그의 제단으로 봉헌한 것이 됐고, 둘째 층대를 목성 마르둑 신에게, 셋째는 화성 네르갈 신에게, 넷째는 태양 샤마쉬에게, 다섯째는 금성 이쉬타르 신에게, 여섯째는 수성 네보 신에게, 그리고 일곱째 층대는 달신 신에게 차례대로 바쳐졌다. (156.3)
여기서 우리는 이 일곱 혹성신들의 배열 순서를 특별히 주목할 것이다. 즉, 토성, 목성, 화성, 태양, 금성, 수성 그리고 달의 순서는 우리가 헬라 사람들이 자랑하는 알렉산드리아의 대천문학자 프톨레마이오스(Klaudios Ptolemaios [Claudius Ptolemaeus] A.D. 120-150?)의 명저인 천문학 대전 알마게스트(Almagest)에 실린 그의 우주관 즉 천동설에 입각한 태양계를 나타내는 천체도에서 볼 수 있기 때문이다. (156.4)
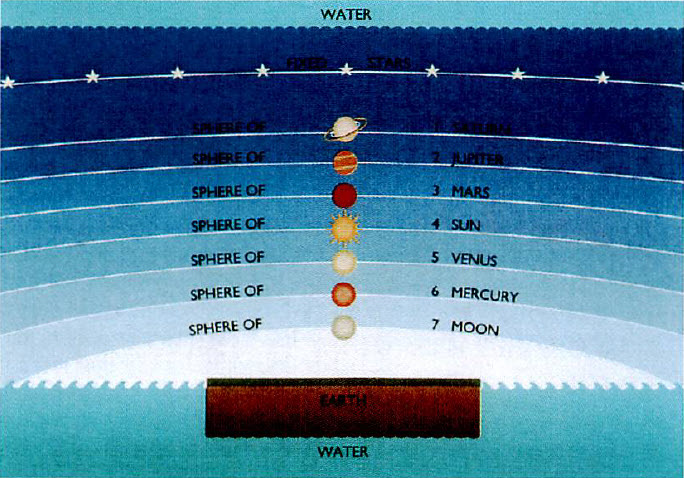
바벨론 사람들의 우주관
아라비아 사람들이 전해주는 전설에 의하면 향년 78세인 대천문학자 프톨레마이오스는 A.D. 127-145년간 천체를 관측했었다고 한다. 모두 13권으로 구성된 그의 명저 알마게스트는 갈릴레오(Galileo Galilei, A.D. 1564-1642)와 코페르니쿠스(Copernicus, A.D. 1473-1543)의 지동설이 1530년에 발표된 이래 그것이 증명될 때까지 근 1,500여 년 동안 천문학의 성경으로 여겨져 왔었다. 그런데 우리는 이 대 천문학자의 명저에서 헬라의 천문학이 바빌로니아의 갈대아 사람들의 점성술에서 상당한 영향을 받았을 뿐만 아니라 오히려 헬라 사람들은 갈대아 사람들의 점성학을 계승 발전시켰다는 사실을 주목해야 할 것이다. (157.1)
오덤은 그의 논문에서 이 지구라트의 모형과 색채 그리고 혹성들의 순차적 배열이 갈대아 사람들의 천동설적인 독특한 우주관을 체계적으로 표현한 것임을 아래와 같이 진술하고 있다: (158.1)
“지구라트 건축물에서 나타난 다음과 같은 혹성들의 배열(태양계) 즉, 토성, 목성, 화성, 태양, 금성, 수성 그리고 달의 순서를 특별히 주의 깊게 주목할 것이다. 토성은 그의 궤도가 가장 긴 것으로 간주되어서 제일 밑바닥에 위치한 가장 큰 층대를 가졌다. 달은 그의 궤도가 짧다고 해서 일곱 번째의 가장 작은 층대가 주어졌다.”51)
그리고 이 혹성들이 태양을 중심으로 두고 배열되었다는 점을 우리는 주목하게 된다. (158.3)